Prime numbers. Somehow boring and yet fascinating topic in mathematics. A number is a prime number if it’s divisible by one and by itself. In contrast composite numbers are divisible by one, itself and one or more other numbers.
Primes: 2, 3, 5, 7, 11, 13...
Composites: 4 = 2 * 2, 6 = 2 * 3, 8 = 2 * 2 * 2, 10 = 2 * 5...
It’s all so simple and obvious when numbers are small. But when the numbers get big, determining how to factorize a large number gets really hard. Really really hard. Seriously hard. Even for a computer. In fact problem of factorization is hard enough to be the basis for asymmetric cryptosistem called RSA.
Wikipedia is very rich with various observations in patterns in prime numbers. Factorization wheels are one of such patterns that are best understood visually. That’s why I created a tiny webapp with Preact that shows a 2-3-5 wheel and 2-3-5-7 wheel.
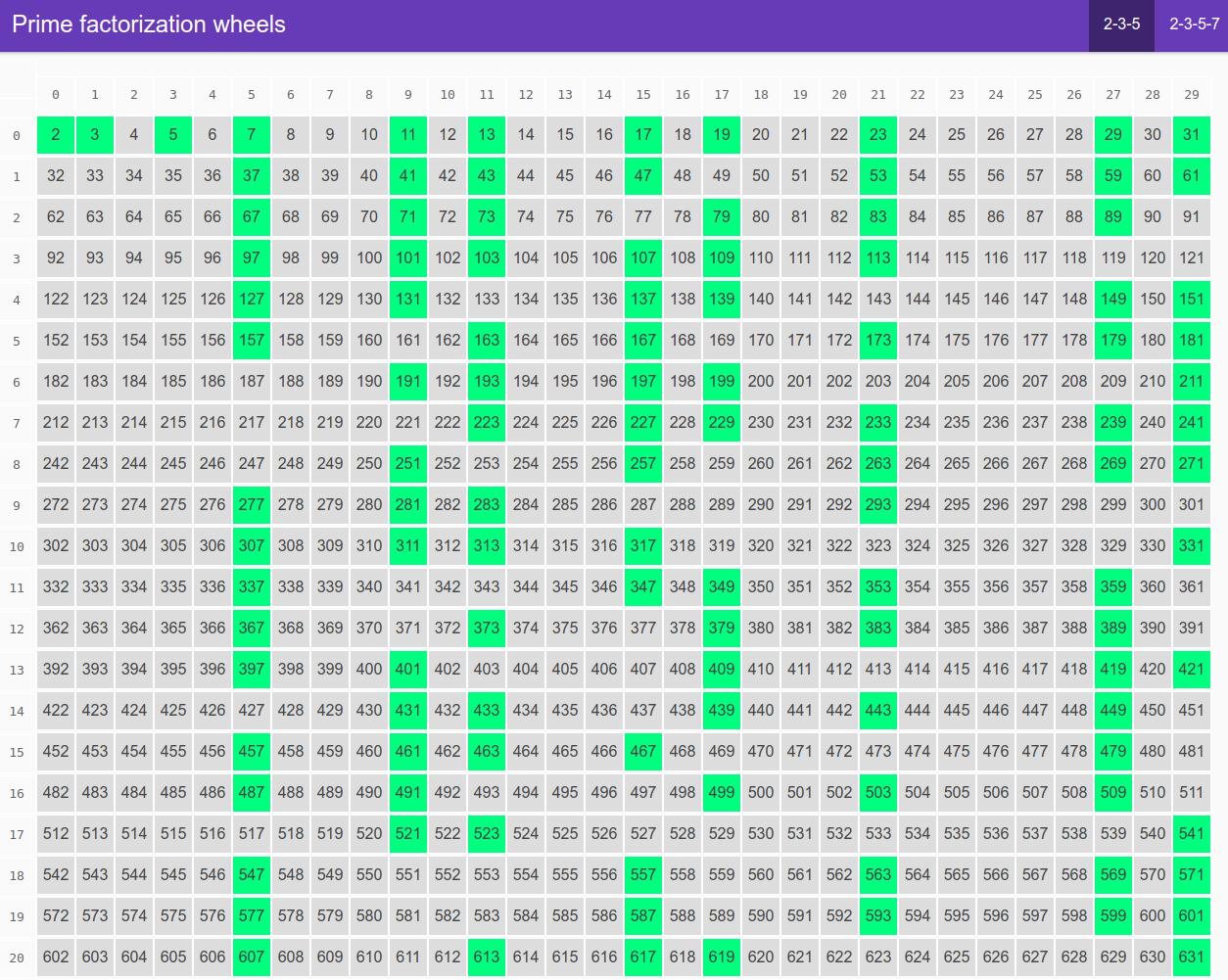
We write numbers one after another. Thirty numbers in each row (because 2 * 3 * 5 = 30). Then we highlight the primes. A convenient pattern emerges. We can see that all the primes (with exception of 2, 3 and 5) are in 8 columns. You can exploit this fact in Sieve of Eratosthenes algorithm for generating a list of primes.
A naive implementation to find prime numbers up to N would require N booleans. That is N bytes of memory. Observing that we actually care only about those 8 columns brings us down to N*8/30 bytes. And packing 8 booleans in a single bytes gets us to N/30 bytes of memory. We just reduced memory consumption of our sieving algorithm by 30 times!
You can also go with a bigger wheel. Next one is 2-3-5-7 wheel with 210 columns. 48 of those contain primes. This means we need 6 bytes per 210 numbers or about 2.9% of memory that would be required for naive implementation with array of booleans. This is a slight improvement over 2-3-5 wheel where we needed 3.3% of memory compared to naive version.
Memory consumption is reduced. What about the speed? Stay tuned for next post where we will see and discuss some benchmarks.